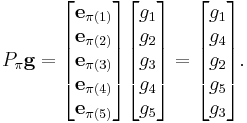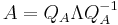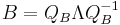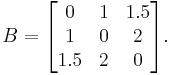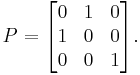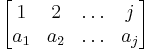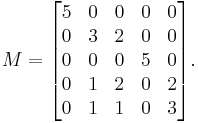Permutation matrix
In mathematics, in matrix theory, a permutation matrix is a square binary matrix that has exactly one entry 1 in each row and each column and 0s elsewhere. Each such matrix represents a specific permutation of m elements and, when used to multiply another matrix, can produce that permutation in the rows or columns of the other matrix.
Contents |
Definition
Given a permutation π of m elements,
given in two-line form by
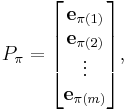
its permutation matrix is the m × m matrix Pπ whose entries are all 0 except that in row i, the entry π(i) equals 1. We may write
where 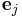 denotes a row vector of length m with 1 in the jth position and 0 in every other position.
denotes a row vector of length m with 1 in the jth position and 0 in every other position.
Properties
Given two permutations π and σ of m elements and the corresponding permutation matrices Pπ and Pσ
This somewhat unfortunate rule is a consequence of the definitions of multiplication of permutations (composition of bijections) and of matrices, and of the choice of using the vectors 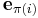 as rows of the permutation matrix; if one had used columns instead then the product above would have been equal to
as rows of the permutation matrix; if one had used columns instead then the product above would have been equal to 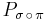 with the permutations in their original order.
with the permutations in their original order.
As permutation matrices are orthogonal matrices (i.e., 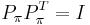 ), the inverse matrix exists and can be written as
), the inverse matrix exists and can be written as
Multiplying 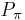 times a column vector g will permute the rows of the vector:
times a column vector g will permute the rows of the vector:
Now applying 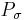 after applying
after applying 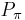 gives the same result as applying
gives the same result as applying 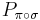 directly, in accordance with the above multiplication rule: call
directly, in accordance with the above multiplication rule: call 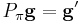 , in other words
, in other words
for all i, then
Multiplying a row vector h times 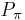 will permute the columns of the vector by the inverse of
will permute the columns of the vector by the inverse of 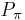 :
:
Again it can be checked that 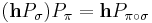 .
.
Notes
Let Sn denote the symmetric group, or group of permutations, on {1,2,...,n}. Since there are n! permutations, there are n! permutation matrices. By the formulas above, the n × n permutation matrices form a group under matrix multiplication with the identity matrix as the identity element.
If (1) denotes the identity permutation, then P(1) is the identity matrix.
One can view the permutation matrix of a permutation σ as the permutation σ of the columns of the identity matrix I, or as the permutation σ−1 of the rows of I.
A permutation matrix is a doubly stochastic matrix. The Birkhoff–von Neumann theorem says that every doubly stochastic matrix is a convex combination of permutation matrices of the same order and the permutation matrices are the extreme points of the set of doubly stochastic matrices. That is, the Birkhoff polytope, the set of doubly stochastic matrices, is the convex hull of the set of permutation matrices.
The product PM, premultiplying a matrix M by a permutation matrix P, permutes the rows of M; row i moves to row π(i). Likewise, MP permutes the columns of M.
The map Sn → A ⊂ GL(n, Z2) is a faithful representation. Thus, |A| = n!.
The trace of a permutation matrix is the number of fixed points of the permutation. If the permutation has fixed points, so it can be written in cycle form as π = (a1)(a2)...(ak)σ where σ has no fixed points, then ea1,ea2,...,eak are eigenvectors of the permutation matrix.
From group theory we know that any permutation may be written as a product of transpositions. Therefore, any permutation matrix P factors as a product of row-interchanging elementary matrices, each having determinant −1. Thus the determinant of a permutation matrix P is just the signature of the corresponding permutation.
Examples
Permutation of rows and columns
When a permutation matrix P is multiplied with a matrix M from the left it will permute the rows of M (here the elements of a column vector),
when P is multiplied with M from the right it will permute the columns of M (here the elements of a row vector):
| reflections | ||
|---|---|---|
|
These arrangements of matrices are reflections of those directly above. |
Permutation of rows
The permutation matrix Pπ corresponding to the permutation :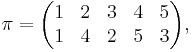 is
is
Given a vector g,
Solving for P
If we are given two matrices A and B which are known to be related as 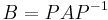 , but the permutation matrix P itself is unknown, we can find P using eigenvalue decomposition:
, but the permutation matrix P itself is unknown, we can find P using eigenvalue decomposition:
where  is a diagonal matrix of eigenvalues, and
is a diagonal matrix of eigenvalues, and  and
and 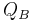 are the matrices of eigenvectors. The eigenvalues of
are the matrices of eigenvectors. The eigenvalues of  and
and  will always be the same, and P can be computed as
will always be the same, and P can be computed as 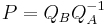 . In other words,
. In other words, 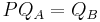 , which means that the eigenvectors of B are simply permuted eigenvectors of A.
, which means that the eigenvectors of B are simply permuted eigenvectors of A.
Example
Let  and
and  be two
be two  matrices such that
matrices such that
Let  be the
be the 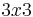 matrix permuting
matrix permuting  into
into  such that
such that
Multiplying  with
with  from the left permutes the rows of
from the left permutes the rows of  whereas and multiplying
whereas and multiplying  from the right permutes the columns of
from the right permutes the columns of  . Therefore
. Therefore  permutes the first and second row and first and second column of
permutes the first and second row and first and second column of  to produce
to produce  (as visual inspection confirms). So
(as visual inspection confirms). So  and
and  share the same eigenvalues by the discussion above. After finding and diagonalizing these eigenvalues, the resultant diagonal matrix
share the same eigenvalues by the discussion above. After finding and diagonalizing these eigenvalues, the resultant diagonal matrix 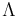 is
is
and the 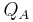 matrix of eigenvectors for
matrix of eigenvectors for  is
is
and the 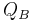 matrix of eigenvectors for
matrix of eigenvectors for  is
is
Comparing the first eigenvector (i.e., the first column) of both we can write the first column of  by noting that the first element (
by noting that the first element (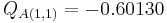 ) matches the second element (
) matches the second element (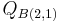 ), thus we put a 1 in the second element of the first column of
), thus we put a 1 in the second element of the first column of  . Repeating this procedure, we match the second element (
. Repeating this procedure, we match the second element (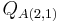 ) to the first element (
) to the first element (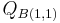 ), thus we put a 1 in the first element of the second column of
), thus we put a 1 in the first element of the second column of  ; and the third element (
; and the third element (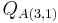 ) to the third element (
) to the third element (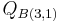 ), thus we put a 1 in the third element of the third column of
), thus we put a 1 in the third element of the third column of  .
.
The resulting  matrix is:
matrix is:
And comparing to the  matrix from above, we find they are the same.
matrix from above, we find they are the same.
Explanation
A permutation matrix will always be in the form
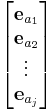
where eai represents the ith basis vector (as a row) for Rj, and where
is the permutation form of the permutation matrix.
Now, in performing matrix multiplication, one essentially forms the dot product of each row of the first matrix with each column of the second. In this instance, we will be forming the dot product of each row of this matrix with the vector of elements we want to permute. That is, for example, v= (g0,...,g5)T,
- eai·v=gai
So, the product of the permutation matrix with the vector v above, will be a vector in the form (ga1, ga2, ..., gaj), and that this then is a permutation of v since we have said that the permutation form is
So, permutation matrices do indeed permute the order of elements in vectors multiplied with them.
Matrices with constant line sums
The sum of the values in each column or row in a permutation matrix adds up to exactly 1. A possible generalization of permutation matrices is nonnegative integral matrices where the values of each column and row add up to a constant number c. A matrix of this sort is known to be the sum of c permutation matrices.
For example in the following matrix M each column or row adds up to 5.
This matrix is the sum of 5 permutation matrices.
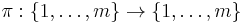
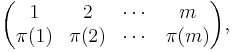
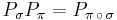
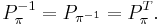
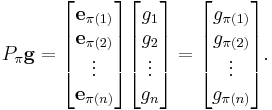
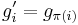
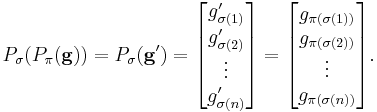
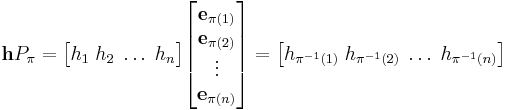
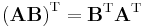 (Compare:
(Compare: